Batch 3 - Class 179 - Circles of Differences
Pre-Class Exercise
- Ten slips of paper, numbered 1 through 10, are placed in a hat. Three numbers are drawn out, one after another. What is the probability that the three numbers are drawn in increasing order?
- Answer: 1/6
Attendance Arjun, Kushagra, Vaazisht, Smiti
Class puzzles
Circles of Differences
The numbers 1,2,3,4 are written on corners of a square. At each step, at midpoint of each side, write the positive difference between numbers at its ends, and join those midpoints to form another square.
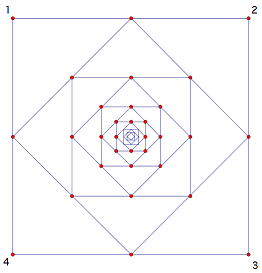
Keep doing this. Eventually, things will get "boring"
- Make a sensible definition of "boring" and determine how many steps it takes for things to get boring.
- It takes 5 steps to go to all zeros. In fact, for any sequence of four evenly spaced numbers (a, a+d, a+2d, a+3d) it would take the same 5 steps.
- Using only integers 0 and 1 at the start, how long can the process go till it gets boring?
- How about if you can use integers 0, 1 or 2?
- 0 through 10? 0 through 100?
- Prove that the process always becomes boring.
- What is true about the largest number in progressive squares?
- Look at subtraction of even/odd with even/odd. Is there a point at which all points become even?
- How far spaced are these even numbers progressively. Do they narrow their difference?
- When you get to all even, the pattern is same as all those numbers divided by 2.
- Where should this lead us?
- Answer: Taking different combinations of even/odd, we can see that all vertices become even in at most 4 steps. Then we can divide by 2, to make the largest number at least half of the original largest number (since numbers can't increase). So you can get to all 0s in most 4 log (max) steps.
- What if you start with 1, 2, pi, 4? How about 1, SQRT(2), pi, 14/3?
- Try to draw invariants - for example, if on a given square, you add/subtract the same number from each vertex, what happens to steps? What if you divide/multiply?
- How do these individual numbers (like pi above) propagate through differences?
- Does this change your proof? That is, did you assume in your proof that all numbers were integers? Did the process still always become boring even if the numbers aren't integers?
- Can you find a set of numbers that do not converge to zeros?
- What if we started with 1,a,a^2,a^3 - what would be the next step (assume a>1)
- Divide the next step by (a-1). This will give us 1,a,a^2,a^2+a+1. This is same as the starting step if a^3=a^2+a+1. This is a cubic equation with one of the solutions as a=1.8393 (approximate)
What if we use other polygons besides square, say an n-sided polygon?
- With n=1 or n=2, things get boring fast - explain why.
- When n=3, you may need to change your definition of boring. Why? Do all sequences become boring in the same way?
- Try to take fibonacci numbers, three consecutive ones of them, and see what happens if you cycle them through this process
- You want to try taking tribonacci numbers (add last three instead of last two) on a square and see what happens? (0,0,1,12,4,7,13...)
- In general, which values of n can use the same definition of boring as the square?
- Note that if n is odd, then the sequence of evens and odds must be imbalanced. Subtracting them would mean that you always are left with at least one even and one add corner. Hence you can never get to all 0s.
- Only n being powers of 2 are guaranteed to get to all 0s. Try on n=6 and n=8 with all zeros and couple of 1s to see what happens.
- Since we know we can create non-converging odd-tuples, for a non-power-of-2-even-number, you can split the sequence into even number of odd-tuples. If you put the non-converging numbers on each of these odd-tuples, by symmetry they will continue to cycle through without converging. So its a question of whether n has an odd factor > 1 - if it does, then the numbers need not converge to 0s.
- Can you establish a general upper limit on how long will it take for a given set of numbers to become boring, based on the largest number in the set and the number of sides in sides of the n-gon?
- Trivial answer: If the largest number doesn't increase, then there are at most MAX^n combinations before a number repeats and gets boring.
This problem has a lot of extensions and beautiful math behind it - See wordplay blog comments referenced below
Homework Problem:
- What is the color of the last square in the following rolling tetrahedron? (Intiial color of base is black)
.png)
- Answer: Black
References: